当前位置: 主页 > 资讯中心 > 公司新闻 » 各优化算法比较,其中的最优收敛值、最差收敛值、平均收敛值,如何计算?从进化图如何看出收敛速度、精度?
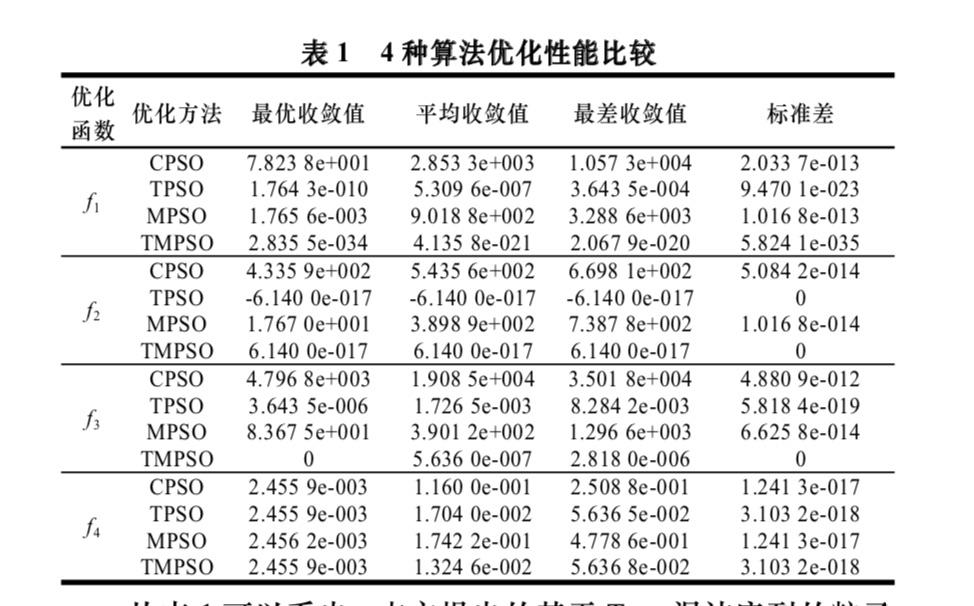
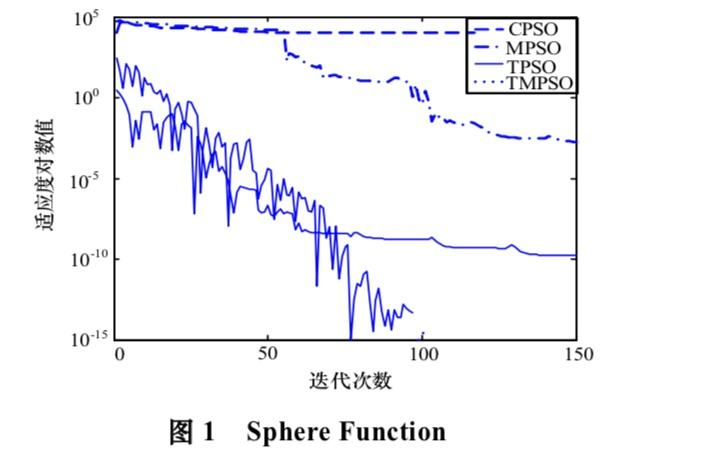
看论文经常看到,比较各优化算法的最优收敛值、最差收敛值和平均收敛值,标准差值,,这些值是如何计算的,见表1,而且文章中通过进化图(见图1),可以看出收敛速度和精度,怎么就能看出来?小弟非常感谢,查了很多文献也查不到,各位大神可以给解释一下吗,或者给小弟个学习方向或者参考资料,小弟愚钝,唯有不耻下问。
谢邀,这个问题挺简单的如果你细心一些读论文应该就能明白。
只谈实验结果分析,那么我们就只看文章的实验部分:包括实验背景,实验设备,参数设置,实验方法等。
其中,参数设置和实验方法应当是你阅读过程中需要关注的重点,而前两者主要是在复现实验时需要注意的重点(如仿真实验的消耗时间对比)
那么我们来讲后两者,我猜你肯定没有获取到全部细节信息以及理解实验方法。这时候你换位思考一下,你现在手头有三个不同的算法,你需要验证一下他们各自的性能,那么你会怎么去设计这个实验?首先是设定一个相同的求解目标,然后让每个算法去对这个目标进行求解,最终比较求解得到的结果精度或者说到达相同精度的时间对吧。相同时间内或相同计算量下谁精度高谁好,相同计算量或相同精度下谁快谁好。
然后如果算法具有随机的性质,那是不是需要考虑一下偶然性?PSO就是典型的基于随机的算法,你用梯度法那就不具备随机性,那么前者你如何消除算法的偶然性?是不是多次求解取平均值?后者没有随机性,是不是就不用去多次求解取平均?说到这儿你应该明白了怎么“计算” 平均值,最大值以及最小值了。
然后看进化曲线,图中的进化曲线实在不是一个好的进化曲线,为什么这么说,因为这哪里是曲线了?处处是拐点,这分明是折线对吧。所以这应该是根据单次实验得出的数据做的图,正确的进化曲线从外观上看应该是平滑的,从数据上看应该是综合了前面为了消除偶然性而进行的所有实验的。如每个算法做了30次实验,那么进化曲线就应该是根据30次里每一代的平均数据而画的图,这个图的平滑程度与实验次数相关,次数越多图越平滑,越具有科学性。
最后,如何从图中看出谁性能好?谁快?
首先你仔细看看横纵坐标分别代表的含义,横轴是进化代数,纵轴是精度。那是不是谁精度高(接近求解目标真正的解),谁更快达到(时间或代数),那就说明该算法性能越好?
论文通常是十分精炼的,每一个信息每一个数据都有意义,题主还需要更加细心和耐心去研读。刚开始不是要多看,而是要学会如何去看。精读一篇文章有时候胜过略读百篇,尤其是初始阶段,学会拆分论文的重点,掌握如何看论文是首先需要研究的。另外,要多采取换位思考的方法,比如你是作者,你要如何去规划一篇文章?你要如何体现出你的工作?你要如何说明你所做的工作有意义?你要如何去打动文章的审稿人?等等。
加油,祝顺利。
表一中:比如算法进行了500次独立重复实验,那么最优收敛值就是算法迭代到停止时,这500次运行结果中最接近真实值的结果;同理,最差收敛值就是算法迭代到停止时,这500次运行结果中最远离真实值的结果;而平均收敛值则为这500次结果的平均值。标准差就是平均收敛值与真实值的方差开根号。
图一中:横坐标为迭代次数,纵坐标为适应度对应值,这里的适应度对应值我觉得是一种评价标准。要评价几个算法求解某个问题的收敛速度,就可以比较谁能更快接近真实值(本问题中为适应度对应值),从图中可以看出,TPSO算法随着迭代次数的增加下降的明显要快一点,因此它的收敛速度要快一些。
这些都是优化算法中的一些基础知识,题主可以多看看优化算法类的基础知识。也可以关注微信公号优化与算法 里面有不少介绍算法原理和算法仿真代码的推文,平时在手机上就可以学习。
请问 题主目前有这方面的代码吗 一起交流学习以下,我也准备做这方面的
?
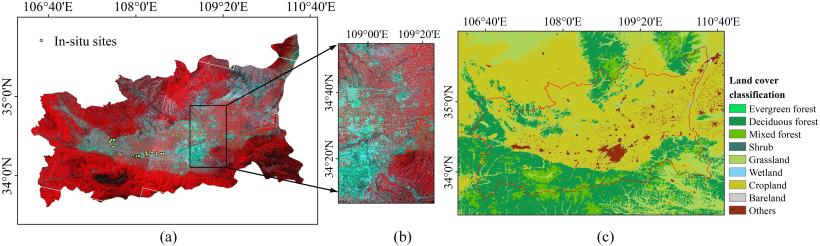
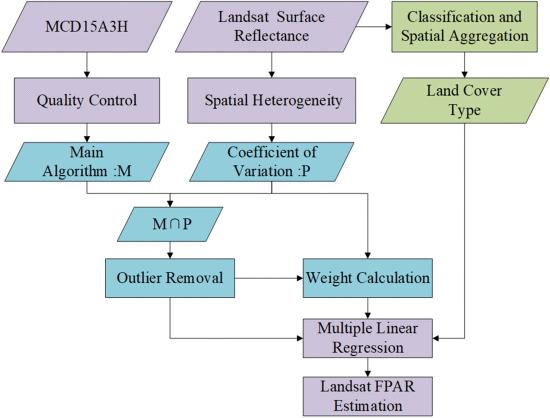
为了在更精细的尺度上对陆地表面过程进行建模,迫切需要对吸收的光合有效辐射(FPAR)的精细分辨率部分进行准确的估计。虽然传统的方法难以兼顾普遍性、效率和准确性,但以粗分辨率产品为参考的方法对细分辨率FPAR的运行估计很有希望。然而,目前的方法面临着粗分辨率FPAR产品中FPAR-反射关系代表性不足的主要问题,特别是对于植被茂密的地区。为了克服这一局限性,本文开发了一种增强的缩放方法,提出了一个去除离群点的程序和一种对所选样本进行加权的方法,并通过粗分辨率FPAR产品和汇总的细分辨率表面反射率之间的加权多元线性回归(MLR)建立FPAR模型。同时,还实施了随机森林回归(RFR)方法进行比较。这两种方法都特别适用于谷歌地球引擎上的Landsat 8 OLI和中等分辨率成像分光仪(MODIS)FPAR数据。它们的性能在区域范围内进行了一整年的测试。增强的缩放方法的结果更接近现场测量(RMSE=0.058和R 2=0.768),与MODIS FPAR(RMSE=0.091和R 2=0.894)相比,与RFR的结果更一致,特别是在植被密集的像素上。这表明一个设计良好的基于MLR的简单方法可以胜过更复杂的RFR方法。与RFR方法相比,增强的缩放方法对训练样本的数量也不太敏感。此外,这两种方法对土地覆盖图都不敏感,其计算效率取决于要估计的图像数量。
?
MCD15A3H.006 MODIS Leaf Area Index/FPAR 4-Day Global 500m
MCD15A3H V6 level 4, Combined Fraction of Photosynthetically Active Radiation (FPAR), and Leaf Area Index (LAI) product是一个为期4天的综合数据集,像素大小为500米。该算法从位于NASA Terra和Aqua卫星上的MODIS传感器在4天内的所有采集中选择 "最佳 "像素。
Dataset Availability
2002-07-04T00:00:00 -
Dataset Provider
NASA LP DAAC at the USGS EROS Center
Collection Snippet
ee.ImageCollection("MODIS/006/MCD15A3H")
?
代码:
/****** This code shows the process of estimating Landat FPAR for the study area by ******/
/****** the enhanced scaling method. Results are NOT realiable due to the reduced amount ******/
/****** of training data (about 5000 samples), the origial training data set contains over ******/
/****** 60000 samples. This code is only intended for ilustrative purposes only. ******/
?
/****** 此代码显示了通过增强缩放方法估算研究区域的 Landat FPAR 的过程。 由于训练数据量减少(约 5000 个样本),结果不可靠,原始训练数据集包含超过 60000 个样本。 此代码仅用于说明目的。 ******/
?
?
//Landsat-8 去云函数
function maskL8sr(image) {
var cloudShadowBitMask = (1 << 3);
var cloudsBitMask = (1 << 5);
var qa = image.select('pixel_qa');
var mask = qa.bitwiseAnd(cloudShadowBitMask).eq(0)
.and(qa.bitwiseAnd(cloudsBitMask).eq(0));
return image.updateMask(mask);
}
?
//进行指定区域影像去云和裁剪
var naip = ee.ImageCollection("LANDSAT/LC08/C01/T1_SR")
.filter(ee.Filter.eq('WRS_PATH', 127))
.filter(ee.Filter.eq('WRS_ROW', 36))
.filterDate('2021-5-30','2021-5-31')
.map(maskL8sr)
.first()
var shp = naip.geometry()
var trueColor432Vis = {
min: 0,
max: 5000,
gamma: 1.1
};
Map.addLayer(naip.select(['B5', 'B4', 'B3']).clip(roi),trueColor432Vis,'RGB')
?
//分类
//获取样本点
var training = naip.sample({
region: shp,
scale: 30,
numPixels: 50000
});
//Kmeans聚类,非监督分类
var clusterer = ee.Clusterer.wekaKMeans(5).train(training);
var result = naip.cluster(clusterer);
Map.centerObject(roi, 12);
?
// MODIS FPAR
var getQABits = function(image, start, end, newName) {
// 计算我们需要提取的位。
var pattern = 0;
for (var i = start; i <= end; i++) {
pattern += Math.pow(2, i);
}
return image.select([0], [newName])
.bitwiseAnd(pattern)
.rightShift(start);
};
?
//MODIS影像
var collection1 = ee.ImageCollection("MODIS/006/MCD15A3H")
.filterDate('2021-5-28','2021-6-3')
.filterBounds(shp)
.select('Fpar','FparLai_QC')
.first()
.clip(shp)
?
var collection = collection1.reproject('EPSG:32649', null, 480);
var QA = collection.select('FparLai_QC');
var landWaterFlag = getQABits(QA, 0,0, 'qc');
var mask = landWaterFlag.neq(0)
var modisProjection = collection.projection();
var Fpar = collection.updateMask(mask.not())
?
//像素聚合,这里选择波段转化系数,方便计算
var naip1 = naip.select('B3').divide(10000)
var naip2 = naip.select('B4').divide(10000)
var naip3 = naip.select('B5').divide(10000)
var naip4 = naip.select('B6').divide(10000)
var naip5 = naip.select('B7').divide(10000)
?
//这里代码可以优化,合并reducer结果
//Landsat 8 各波段进行重分类,分别计算标准差
var std1 = naip1
.reduceResolution({
reducer: ee.Reducer.stdDev(),
maxPixels: 1024
})
.reproject({
crs: modisProjection
});
//平均值
var Mean1 = naip1
.reduceResolution({
reducer: ee.Reducer.mean(),
maxPixels: 1024
})
.reproject({
crs: modisProjection
});
?
var std2 = naip2
.reduceResolution({
reducer: ee.Reducer.stdDev(),
maxPixels: 1024
})
.reproject({
crs: modisProjection
});
var Mean2 = naip2
.reduceResolution({
reducer: ee.Reducer.mean(),
maxPixels: 1024
})
.reproject({
crs: modisProjection
});
var std3 = naip3
.reduceResolution({
reducer: ee.Reducer.stdDev(),
maxPixels: 1024
})
.reproject({
crs: modisProjection
});
var Mean3 = naip3
.reduceResolution({
reducer: ee.Reducer.mean(),
maxPixels: 1024
})
.reproject({
crs: modisProjection
});
var std4 = naip4
.reduceResolution({
reducer: ee.Reducer.stdDev(),
maxPixels: 1024
})
.reproject({
crs: modisProjection
});
var Mean4 = naip4
.reduceResolution({
reducer: ee.Reducer.mean(),
maxPixels: 1024
})
.reproject({
crs: modisProjection
});
var std5 = naip5
.reduceResolution({
reducer: ee.Reducer.stdDev(),
maxPixels: 1024
})
.reproject({
crs: modisProjection
});
var Mean5 = naip5
.reduceResolution({
reducer: ee.Reducer.mean(),
maxPixels: 1024
})
.reproject({
crs: modisProjection
});
?
var land = result
.reduceResolution({
reducer: ee.Reducer.mode(),
maxPixels: 1024
})
.reproject({
crs: modisProjection
});
//加载训练数据
var train_data = ee.FeatureCollection('users/43012496/traing_fpar/Train_demo')
var fpar_manzu = Fpar.select('Fpar').clip(train_data)
var fpar_quanzhong = fpar_manzu.multiply(0.01)
?
//计算权重,掩膜掉大于0.9的部分,进行像素统计
var fp9 = fpar_quanzhong.updateMask(fpar_quanzhong.gte(0.9)).reduceRegion({
reducer: ee.Reducer.count(),
geometry: shp,
scale: 480,
crs: 'EPSG:32649',
maxPixels: 11e9
})
//计算权重,掩膜掉大于0.8的部分,进行像素统计
var fp8 = fpar_quanzhong.updateMask(fpar_quanzhong.gte(0.8)).reduceRegion({
reducer: ee.Reducer.count(),
geometry: shp,
scale: 480,
crs: 'EPSG:32649',
maxPixels: 11e9
})
//
var a2 = fp9.getNumber('Fpar')
var a3 = fp8.getNumber('Fpar')
var num1 = ee.Number(1)
var per = num1.add(num1.subtract(a2.divide(a3)))
var fpar_quan = fpar_quanzhong.where(fpar_quanzhong.lt(0.9),1)
.where(fpar_quanzhong.gte(0.9),per)
var img = land.updateMask(fpar_manzu.select('Fpar'))
?
//不同土地覆盖类型的多元线性回归
var manzu = fpar_manzu.select('Fpar').multiply(0.01).addBands(img.rename('biome'))
var manzu1 = manzu.updateMask(manzu.select('biome').eq(0)).select('Fpar')
var manzu2 = manzu.updateMask(manzu.select('biome').eq(1)).select('Fpar')
var manzu3 = manzu.updateMask(manzu.select('biome').eq(2)).select('Fpar')
var manzu4 = manzu.updateMask(manzu.select('biome').eq(3)).select('Fpar')
var manzu5 = manzu.updateMask(manzu.select('biome').eq(4)).select('Fpar')
?
var biome01 = Mean1.updateMask(manzu.select('biome').eq(0))
var biome02 = Mean2.updateMask(manzu.select('biome').eq(0))
var biome03 = Mean3.updateMask(manzu.select('biome').eq(0))
var biome04 = Mean4.updateMask(manzu.select('biome').eq(0))
var biome05 = Mean5.updateMask(manzu.select('biome').eq(0))
?
var biome11 = Mean1.updateMask(manzu.select('biome').eq(1))
var biome12 = Mean2.updateMask(manzu.select('biome').eq(1))
var biome13 = Mean3.updateMask(manzu.select('biome').eq(1))
var biome14 = Mean4.updateMask(manzu.select('biome').eq(1))
var biome15 = Mean5.updateMask(manzu.select('biome').eq(1))
var biome21 = Mean1.updateMask(manzu.select('biome').eq(2))
var biome22 = Mean2.updateMask(manzu.select('biome').eq(2))
var biome23 = Mean3.updateMask(manzu.select('biome').eq(2))
var biome24 = Mean4.updateMask(manzu.select('biome').eq(2))
var biome25 = Mean5.updateMask(manzu.select('biome').eq(2))
var biome31 = Mean1.updateMask(manzu.select('biome').eq(3))
var biome32 = Mean2.updateMask(manzu.select('biome').eq(3))
var biome33 = Mean3.updateMask(manzu.select('biome').eq(3))
var biome34 = Mean4.updateMask(manzu.select('biome').eq(3))
var biome35 = Mean5.updateMask(manzu.select('biome').eq(3))
var biome41 = Mean1.updateMask(manzu.select('biome').eq(4))
var biome42 = Mean2.updateMask(manzu.select('biome').eq(4))
var biome43 = Mean3.updateMask(manzu.select('biome').eq(4))
var biome44 = Mean4.updateMask(manzu.select('biome').eq(4))
var biome45 = Mean5.updateMask(manzu.select('biome').eq(4))
var constant = ee.Image(1)
?
//训练 MLR 模型
//这里是将多波段分别合并不同的参数
var imgRegress0 = ee.Image.cat(constant,biome01,biome02,biome03,biome04,biome05, manzu1).multiply(fpar_quan)
var imgRegress1 = ee.Image.cat(constant,biome11,biome12,biome13,biome14,biome15, manzu2).multiply(fpar_quan)
var imgRegress2 = ee.Image.cat(constant,biome21,biome22,biome23,biome24,biome25, manzu3).multiply(fpar_quan)
var imgRegress3 = ee.Image.cat(constant,biome31,biome32,biome33,biome34,biome35, manzu4).multiply(fpar_quan)
var imgRegress4 = ee.Image.cat(constant,biome41,biome42,biome43,biome44,biome45, manzu5).multiply(fpar_quan)
?
//进行线性回归分析,这里用的linearRegression
var linearRegression0 = imgRegress0.reduceRegion({
reducer: ee.Reducer.linearRegression({
numX: 6,
numY: 1
}),
geometry: shp,
scale: 480,
tileScale: 16
});
var linearRegression1 = imgRegress1.reduceRegion({
reducer: ee.Reducer.linearRegression({
numX: 6,
numY: 1
}),
geometry: shp,
scale: 480,
tileScale: 16
});
var linearRegression2 = imgRegress2.reduceRegion({
reducer: ee.Reducer.linearRegression({
numX: 6,
numY: 1
}),
geometry: shp,
scale: 480,
tileScale: 16
});
var linearRegression3 = imgRegress3.reduceRegion({
reducer: ee.Reducer.linearRegression({
numX: 6,
numY: 1
}),
geometry: shp,
scale: 480,
tileScale: 16
});
var linearRegression4 = imgRegress4.reduceRegion({
reducer: ee.Reducer.linearRegression({
numX: 6,
numY: 1
}),
geometry: shp,
scale: 480,
tileScale: 16
});
?
//得到系数,然后分别获取每一个系数,得到系数这里得转化为列表
var coefList0 = ee.Array(linearRegression0.get('coefficients')).toList();
var a0 = ee.List(coefList0.get(0)).get(0);
var a1 = ee.List(coefList0.get(1)).get(0);
var a2 = ee.List(coefList0.get(2)).get(0);
var a3 = ee.List(coefList0.get(3)).get(0);
var a4 = ee.List(coefList0.get(4)).get(0);
var a5 = ee.List(coefList0.get(5)).get(0);
var coefList1 = ee.Array(linearRegression1.get('coefficients')).toList();
var b0 = ee.List(coefList1.get(0)).get(0);
var b1 = ee.List(coefList1.get(1)).get(0);
var b2 = ee.List(coefList1.get(2)).get(0);
var b3 = ee.List(coefList1.get(3)).get(0);
var b4 = ee.List(coefList1.get(4)).get(0);
var b5 = ee.List(coefList1.get(5)).get(0);
var coefList2 = ee.Array(linearRegression2.get('coefficients')).toList();
var c0 = ee.List(coefList2.get(0)).get(0);
var c1 = ee.List(coefList2.get(1)).get(0);
var c2 = ee.List(coefList2.get(2)).get(0);
var c3 = ee.List(coefList2.get(3)).get(0);
var c4 = ee.List(coefList2.get(4)).get(0);
var c5 = ee.List(coefList2.get(5)).get(0);
var coefList3 = ee.Array(linearRegression3.get('coefficients')).toList();
var d0 = ee.List(coefList3.get(0)).get(0);
var d1 = ee.List(coefList3.get(1)).get(0);
var d2 = ee.List(coefList3.get(2)).get(0);
var d3 = ee.List(coefList3.get(3)).get(0);
var d4 = ee.List(coefList3.get(4)).get(0);
var d5 = ee.List(coefList3.get(5)).get(0);
var coefList4 = ee.Array(linearRegression4.get('coefficients')).toList();
var e0 = ee.List(coefList4.get(0)).get(0);
var e1 = ee.List(coefList4.get(1)).get(0);
var e2 = ee.List(coefList4.get(2)).get(0);
var e3 = ee.List(coefList4.get(3)).get(0);
var e4 = ee.List(coefList4.get(4)).get(0);
var e5 = ee.List(coefList4.get(5)).get(0);
?
//选择波段,分别获取不同
var land0 = naip.select(['B3','B4','B5','B6','B7']).updateMask(result.eq(0)).multiply(0.0001)
var land1 = naip.select(['B3','B4','B5','B6','B7']).updateMask(result.eq(1)).multiply(0.0001)
var land2 = naip.select(['B3','B4','B5','B6','B7']).updateMask(result.eq(2)).multiply(0.0001)
var land3 = naip.select(['B3','B4','B5','B6','B7']).updateMask(result.eq(3)).multiply(0.0001)
var land4 = naip.select(['B3','B4','B5','B6','B7']).updateMask(result.eq(4)).multiply(0.0001)
?
//Landsat FPAR 估计
function FPAR0(land0) {
var B3 = land0.select("B3");
var B4 = land0.select("B4");
var B5 = land0.select("B5");
var B6 = land0.select("B6");
var B7 = land0.select("B7");
?
//这里利用一景选择好的参数建立一个多源线性回归分析
var fpar = land0.expression(
"a0+(a1*B3)+(a2*B4)+(a3*B5)+(a4*B6)+(a5*B7)",
{
"B3": B3,
"B4": B4,
"B5": B5,
"B6": B6,
"B7": B7,
"a0": ee.Number(a0),
"a1": ee.Number(a1),
"a2": ee.Number(a2),
"a3": ee.Number(a3),
"a4": ee.Number(a4),
"a5": ee.Number(a5),
}
);
return fpar;
}
function FPAR1(land1) {
var B3 = land1.select("B3");
var B4 = land1.select("B4");
var B5 = land1.select("B5");
var B6 = land1.select("B6");
var B7 = land1.select("B7");
var fpar = land1.expression(
"b0+(b1*B3)+(b2*B4)+(b3*B5)+(b4*B6)+(b5*B7)",
{
"B3": B3,
"B4": B4,
"B5": B5,
"B6": B6,
"B7": B7,
"b0": ee.Number(b0),
"b1": ee.Number(b1),
"b2": ee.Number(b2),
"b3": ee.Number(b3),
"b4": ee.Number(b4),
"b5": ee.Number(b5),
}
);
return fpar;
}
function FPAR2(land2) {
var B3 = land2.select("B3");
var B4 = land2.select("B4");
var B5 = land2.select("B5");
var B6 = land2.select("B6");
var B7 = land2.select("B7");
var fpar = land2.expression(
"c0+(c1*B3)+(c2*B4)+(c3*B5)+(c4*B6)+(c5*B7)",
{
"B3": B3,
"B4": B4,
"B5": B5,
"B6": B6,
"B7": B7,
"c0": ee.Number(c0),
"c1": ee.Number(c1),
"c2": ee.Number(c2),
"c3": ee.Number(c3),
"c4": ee.Number(c4),
"c5": ee.Number(c5),
}
);
return fpar;
}
function FPAR3(land3) {
var B3 = land3.select("B3");
var B4 = land3.select("B4");
var B5 = land3.select("B5");
var B6 = land3.select("B6");
var B7 = land3.select("B7");
var fpar = land3.expression(
"d0+(d1*B3)+(d2*B4)+(d3*B5)+(d4*B6)+(d5*B7)",
{
"B3": B3,
"B4": B4,
"B5": B5,
"B6": B6,
"B7": B7,
"d0": ee.Number(d0),
"d1": ee.Number(d1),
"d2": ee.Number(d2),
"d3": ee.Number(d3),
"d4": ee.Number(d4),
"d5": ee.Number(d5),
}
);
return fpar;
}
function FPAR4(land4) {
var B3 = land4.select("B3");
var B4 = land4.select("B4");
var B5 = land4.select("B5");
var B6 = land4.select("B6");
var B7 = land4.select("B7");
var fpar = land4.expression(
"e0+(e1*B3)+(e2*B4)+(e3*B5)+(e4*B6)+(e5*B7)",
{
"B3": B3,
"B4": B4,
"B5": B5,
"B6": B6,
"B7": B7,
"e0": ee.Number(e0),
"e1": ee.Number(e1),
"e2": ee.Number(e2),
"e3": ee.Number(e3),
"e4": ee.Number(e4),
"e5": ee.Number(e5),
}
);
return fpar;
}
?
//重命名
var fpar0 = FPAR0(land0).rename('fpar')
var fpar1 = FPAR1(land1).rename('fpar')
var fpar2 = FPAR2(land2).rename('fpar')
var fpar3 = FPAR3(land3).rename('fpar')
var fpar4 = FPAR4(land4).rename('fpar')
var visParam = {
min: 0,
max: 100,
palette: 'FFFFFF, CE7E45, DF923D, F1B555, FCD163, 99B718, 74A901, 66A000, 529400,' +
'3E8601, 207401, 056201, 004C00, 023B01, 012E01, 011D01, 011301'
};
?
//镶嵌五种土地覆盖类型
var mask = fpar0.mask().or(fpar1.mask()).or(fpar2.mask()).or(fpar3.mask()).or(fpar4.mask());
var baseImg = ee.Image.constant(0)
.updateMask(mask);
var newImgA = baseImg.where(fpar0.mask(), fpar0);
var newImgD = baseImg.where(fpar1.mask(), fpar1);
var newImgB = baseImg.where(fpar2.mask(), fpar2);
var newImgC = baseImg.where(fpar3.mask(), fpar3);
var newImgE = baseImg.where(fpar4.mask(), fpar4);
var union = newImgA.add(newImgB).add(newImgC).add(newImgD).add(newImgE);
?
//展示结果
var fpar = union.multiply(100).round().clip(roi)
Map.addLayer(fpar, visParam, "FPAR");
本文以MODIS FPAR产品为参考,开发了一种集成了离群点去除程序和MLR中样本加权方法的增强型比例尺方法,用于业务精细分辨率FPAR的估算。提出的基于加权MLR的增强型比例尺方法与GEE上的RFR方法进行了比较,在大关中地区应用于预测2020年9月至2021年8月一整年的Landsat FPAR图像。主要结论如下。
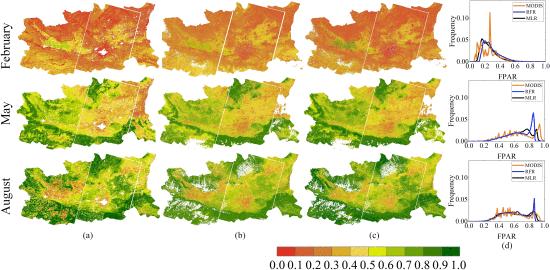
强化比例尺法和RFR法都产生了与MODIS一致的、空间上一致的精细分辨率FPAR。RFR方法高估了低FPAR值,低估了高FPAR值,而增强缩放法的表现优于RFR方法。特别是,在增强的缩放方法中,密集植被像素的高FPAR值被低估的情况明显改善。
强化比例尺法和RFR法都用原地FPAR测量值进行了验证。增强的缩放方法比RFR方法表现更好,特别是对于植被茂密的像素。RFR和增强型缩放方法的总体RMSE值分别为0.049和0.046,总体R2值为0.685和0.768。
增强的缩放方法对训练样本不太敏感,而RFR方法对训练样本的依赖程度较高。强化比例尺法更容易实现,只需一对MODIS-Landsat图像,在同质和异质像素上都比RFR法更准确。
?
数据引用:
Wang Y, Zhan Y, Yan G, et al. Generalized Fine-Resolution FPAR Estimation Using Google Earth Engine: Random Forest or Multiple Linear Regression[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2022, 16: 918-929.
?GEE:基于不同光谱指数、地形特征等组合的多种机器学习方法实现土地分类(安第斯高原)
GEE:西非沿海地区脆弱性数据集(社会脆弱性、人口风险、以及贫困和适应能力)
GEE:使用MODIS数据(FVC/LAI/FAPAR/CWC)和随机森林方法完成全球生物量估算(含代码)
